A central task of civil aerospace is to develop more energy- and material-efficient, and less noisy propulsion systems. A substantial challenge is the susceptibility to vibrations of the lighter and aerodynamically highly loaded components. We advance the fundamental understanding of vibration phenomena, develop approaches for vibration prediction, and develop more effective concepts for vibration mitigation. This way, we contribute to extending the feasible design space and the range of tolerable operating conditions, without sacrificing the high demands for strength and durability.
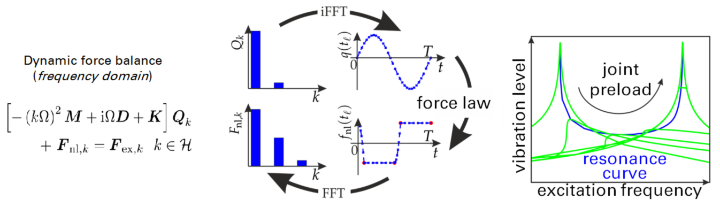
We focus on nonlinear vibrations of mechanical systems with friction and impacts. Such strong nonlinearities lead to amplitude dependence of vibration characteristics, cause additional resonances, bound otherwise unstable vibrations and make the steady vibration state dependent on the initial conditions. We develop computational methods for vibration prediction. In our vibration laboratory, we test the methods we develop for modal analysis of nonlinear systems and validate our simulations. We enjoy the synergetic relation between fundamental research funded by DFG, MWK and foundations, and application-oriented research in close collaboration with our industry partners.
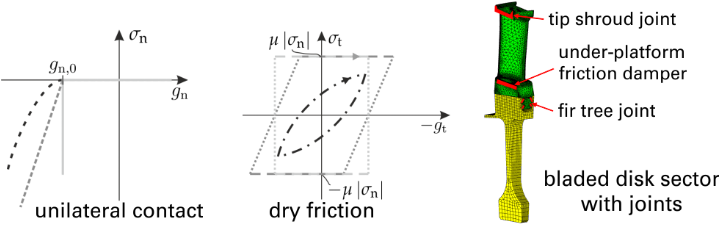
Jointed Structures
In lightweight structures, the dry sliding friction in mechanical joints is often the main dissipation mechanism (friction damping). Moreover, impacts may occur. These strongly nonlinear interactions cause a dependence of the joint’s effective stiffness and damping on the vibration level and give rise to intriguing vibration phenomena that cannot be explained by linear theory.
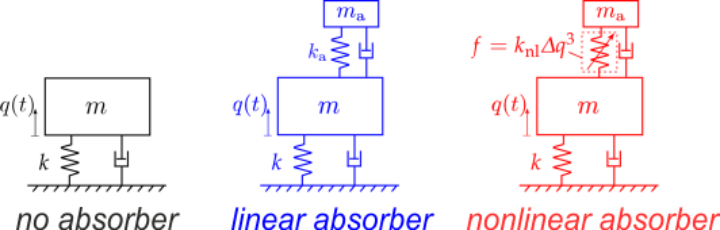
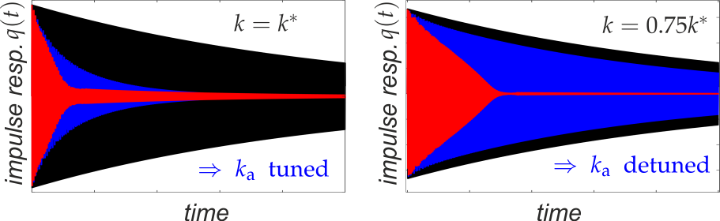
Nonlinear Vibration Absorbers
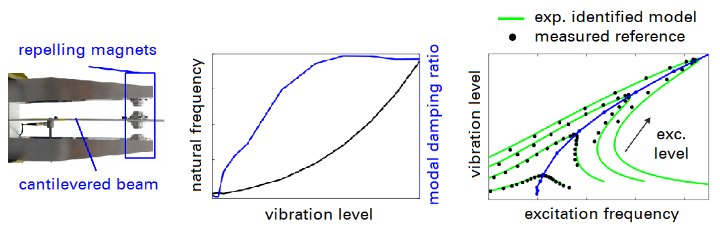
Nonlinear Modal Analysis
Damping is an essential aspect in structural dynamics, and it is often nonlinear. Almost all available testing methods rely on linear theory and yield erroneous results in the nonlinear case. We develop methods for accurate and robust experimental and numerical quantification of damping, natural frequencies and modal deflection shapes as function of the vibration level.
Development of Simulation Methods
Capabilities
- Harmonic Balance
- Shooting & Time Stepping
- Numerical Path Continuation
- Component Mode Synthesis
- Model Order Reduction
We have developed a simple Matlab Tool for the simulation of nonlinear vibrations, which is publically available on the NLvib subsite. It includes Harmonic Balance, Shooting Method, path continuation and nonlinear modal analysis.
Teaching
We offer various lectures, exercises and seminars on
- Structural Dynamics,
- Nonlinear Structural Dynamics,
- Turbomachinery Blade Vibrations and
- Structural Mechanics of Aircraft Engines.
Our Network
We have research projects with distinguished national and international academic partners in the areas of aero-elasticity, damage mechanics, tribology and nonlinear dynamics.The professorship is part of the university’s center of competence with MTU Aero Engines.
Are you interested in contributing to our activities?
Depending on the current stage of your academic education, you may apply for a position as a doctoral researcher, student assistant or for a Bachelor/Master thesis.
We also offer opportunities for postdoctoral researchers with appropriate scientific profile and track record. Due to the time lines of certain prestigious scholarships, we recommend to contact us about 1 year prior the start of your planned visit.
Publications
Gross, J.; Gupta, V.; Berthold, C.; Krack, M.: A new paradigm for multi-fidelity continuation using parallel model refinement. Computer Methods in Applied Mechanics and Engineering, 2024. doi: 10.1016/j.cma.2024.116860
Woiwode, L.; Krack, M.: Experimentally uncovering isolas via backbone tracking. Journal of Structural Dynamics, 2024. doi: 10.25518/2684-6500.180
Müller, F.; Krack, M.: On the locomotion of the slider within a self-adaptive beam-slider system. International Journal of Non-Linear Mechanics, 2023. doi: 10.1016/j.ijnonlinmec.2023.104595
Weidemann, T.; Carassale, L.; Denoel, V.; Krack, M.: On the broadband efficacy of impact absorbers. Journal of Sound and Vibration, 2024. doi: 10.1016/j.jsv.2023.118161
Schwarz, S.; Reil, J.; Gross, J.; Hartung, A.; Rittinger, D.; Krack, M.: Friction Saturated Limit Cycle Oscillations - Test Rig Design and Validation of Numerical Prediction Methods. J. Eng. Gas Turbines Power, 2023. doi: 10.1115/1.4063769
Ferhatoglu, E.; Groß, J.; Krack, M.: Frequency response variability in friction-damped structures due to non-unique residual tractions: Obtaining conservative bounds using a nonlinear-mode-based approach. Mechanical Systems and Signal Processing, 2023. doi: 10.1016/j.ymssp.2023.110651
Woiwode, L.; Krack, M.: Are Chebyshev-based stability analysis and Urabe’s error bound useful features for Harmonic Balance? Mechanical Systems and Signal Processing 194, 2023. doi: 10.1016/j.ymssp.2023.110265
Theurich, T.; Krack, M.: Experimental validation of impact energy scattering as concept for mitigating resonant vibrations. Journal of Structural Dynamics, 2023. doi: 10.25518/2684-6500.126
Müller, F.; Beck, M.; Krack, M.: Experimental validation of a model for a self-adaptive beam–slider system. Mechanical Systems and Signal Processing 182, 2023. doi: 10.1016/j.ymssp.2022.109551
Berthold, C.; Gross, J.; Frey, C.; Krack, M.: Fully Coupled Analysis of Flutter Induced Limit Cycles: Frequency Versus Time Domain Methods. J. Eng. Gas Turbines Power, 2023. doi: 10.1115/1.4062408
Seeger, B.; Kohlmann, L.; Schoenenborn, H.; Schwarz, S.; Krack, M.: Identification of Mistuning Based On Forced Response Measurements and Assessment for a Real Compressor Blisk. J. Eng. Gas Turbines Power, 2022. doi: 10.1115/1.4055019
Monjaraz-Tec, C.; Kohlmann, L.; Schwarz, S.; Hartung, A.; Gross, J.; Krack, M.: Prediction and validation of the strongly modulated forced response of two beams undergoing frictional impacts. Mechanical Systems and Signal Processing 180, 2022. doi: 10.1016/j.ymssp.2022.109410
Gehr, F.; Theurich, T.; Monjaraz-Tec, C.; Gross, J.; Schwarz, S.; Hartung, A.; Krack, M.: Computational and experimental analysis of the impact of a sphere on a beam and the resulting modal energy distribution. Mechanical Systems and Signal Processing 180, 2022. doi: 10.1016/j.ymssp.2022.109407
Müller, F.; Woiwode, L.; Gross, J.; Scheel, M.; Krack, M.: Nonlinear damping quantification from phase-resonant tests under base excitation. Mechanical Systems and Signal Processing, 2022. doi: 10.1016/j.ymssp.2022.109170
Chen, J.; Theurich, T.; Krack, M.; Sapsis, T.; Bergman, L.A.; Vakakis, A.F.: Intense cross-scale energy cascades resembling “mechanical turbulence” in harmonically driven strongly nonlinear hierarchical chains of oscillators. Acta Mechanica 233(4), 2022. doi: 10.1007/s00707-022-03159-w
Abeloos, G.; Müller, F.; Ferhatoglu, E.; Scheel, M.; Collette, C.; Kerschen, G.; Brake, M.R.W.; Tiso, P.; Renson, L.; Krack, M.: A consistency analysis of phase-locked-loop testing and control-based continuation for a geometrically nonlinear frictional system. Mechanical Systems and Signal Processing 170, 2022. doi: 10.1016/j.ymssp.2022.108820
Woiwode, L.; Müller, F.; Gross, J.; Scheel, M.; Krack, M.: How Intrusive Are Accelerometers for Measuring Nonlinear Vibrations? A Case Study on a Compressor Blade Subjected to Vibro-Impact Dynamics? Journal of Vibration and Acoustics 144(4), 2022.doi: 10.1115/1.4053357
Monjaraz-Tec, C. D.; Gross, J.; Krack, M.: A massless boundary component mode synthesis method for elastodynamic contact problems. Computers and Structures, 2022. doi: 10.1016/j.compstruc.2021.106698
Theurich, T.; Vakakis, A.F.; Krack, M.: Predictive design of impact absorbers for mitigating resonances of flexible structures using a semi-analytical approach. Journal of Sound and Vibration, 2021. doi: 10.1016/j.jsv.2021.116527
Woiwode, L.; Vakakis, A.F.; Krack, M.: Analysis of the non-periodic oscillations of a self-excited friction-damped system with closely spaced modes. Nonlinear Dynamics 164, 2021. doi: 10.1007/s11071-021-06893-3
Krack, M.: Extension of the single-nonlinear-mode theory by linear attachments and application to exciter-structure interaction. Journal of Sound and Vibration 505, 2021. doi: 10.1016/j.jsv.2021.116120
Dreher, T.; Brake, M.R.W.; Seeger, B.; Krack, M.: In situ, real-time measurements of contact pressure internal to jointed interfaces during dynamic excitation of an assembled structure. Mechanical Systems and Signal Processing 160, 2021. doi: 10.1016/j.ymssp.2021.107859
Berthold, C.; Gross, J.; Frey, C.; Krack, M.: Development of a fully-coupled harmonic balance method and a refined energy method for the computation of flutter-induced Limit Cycle Oscillations of bladed disks with nonlinear friction contacts. Journal of Fluids and Structures (102), 2021. doi: 10.1016/j.jfluidstructs.2021.103233
Balaji, N.N.; Dreher, T.; Krack, M.; Brake, M.R.W.: Reduced order modeling for the dynamics of jointed structures through hyper-reduced interface representation. Mechanical Systems and Signal Processing 149, 2021. doi: 10.1016/j.ymssp.2020.107249
Gastaldi, C.; Scheel, M.; Gross, J.; Berruti, T.; Krack, M.: Modeling Complex Contact Conditions and Their Effect On Blade Dynamics. J. Eng. Gas Turbines Power 143(1), 2020. doi: 10.1115/1.4049186
Balaji, N.N.; Lian, S.; Scheel, M.; Brake, M.R.W.; Tiso, P.; Noël, J.-P.; Krack, M.: Numerical Assessment of Polynomial Nonlinear State-Space and Nonlinear-Mode Models for Near-Resonant Vibrations. Vibration 3(3), 2020. doi: 10.3390/vibration3030022
Woiwode, L.; Gross, J.; Krack, M.: Effect of Modal Interactions on Friction-Damped Self-Excited Vibrations. Journal of Vibration and Acoustics 143(3), 2020. doi: 10.1115/1.4048396
Berthold, C.; Gross, J.; Frey, C.; Krack, M.: Analysis of Friction-Saturated Flutter Vibrations With a Fully Coupled Frequency Domain Method. J. Eng. Gas Turbines Power 142(11), 2020. doi: 10.1115/1.4048650
Gross, J.; Krack, M.: Multi-Wave Flutter Vibrations in Mistuned Cascades with Tip-Shroud Friction. J. Eng. Gas Turbines Power, 2020. doi: 10.1115/1.4047889
Scheel, M.; Weigele, T.; Krack, M.: Challenging an experimental nonlinear modal analysis method with a new strongly friction-damped structure. Journal of Sound and Vibration 485, 2020. doi: 10.1016/j.jsv.2020.115580
Fang, B.; Theurich, T.; Krack, M.; Bergman, L.A.; Vakakis, A. F.: Vibration suppression and modal energy transfers in a linear beam with attached vibro-impact nonlinear energy sinks. Communications in Nonlinear Science and Numerical Simulation 91, 2020. doi: 10.1016/j.cnsns.2020.105415
Scheel, M.; Kleyman, G.; Tatar, A.; Brake, M.R.W.; Peter, S.; Noël, J.-P.; Allen, M.S.; Krack, M.: Experimental assessment of polynomial nonlinear state-space and nonlinear-mode models for near-resonant vibrations. Mechanical Systems and Signal Processing 143, 2020. doi: 10.1016/j.ymssp.2020.106796
Müller, F.; Krack, M.: Explanation of the self-adaptive dynamics of a harmonically forced beam with a sliding mass. Archive of Applied Mechanics, 2020. doi: 10.1007/s00419-020-01684-5
Woiwode, L.; Balaji, N.N.; Kappauf, J.; Tubita, F.; Guillot, L.; Vergez, C.; Cochelin, B.; Grolet, A.; Krack, M.: Comparison of two algrithms for Harmonic Balance and path continuation. Mechanical Systems and Signal Processing 136, 2020. doi: 10.1016/j.ymssp.2019.106503
Gross, J.; Krack, M.: Multi-Wave Vibration Caused by Flutter Instability and Nonlinear Tip Shroud Friction. J. Eng. Gas Turbines Power, 2019. doi: 10.1115/1.4044884
Schwarz, S.; Kohlmann, L.; Hartung, A.; Gross, J.; Scheel, M.; Krack, M.: Validation of A Turbine Blade Component Test with Frictional Contacts by Phase-Locked-Loop and Force-Controlled Measurements. J. Eng. Gas Turbines Power, 2019. doi: 10.1115/1.4044772
Theurich, T.; Gross, J.; Krack, M.: Effects of modal energy scattering and friction on the resonance mitigation with an impact absorber. Journal of Sound and Vibration 442, 71-89, 2019. doi: 10.1016/j.jsv.2018.10.055
Scheel, M.; Peter, S.; Leine, R.I.; Krack, M.: A phase resonance approach for modal testing of structures with nonlinear dissipation. Journal of Sound and Vibration 435, 56-73, 2018. doi: 10.1016/j.jsv.2018.07.010
Hartung, A.; Hackenberg, H.-P.; Krack, M.; Groß, J.; Heinze, T.; Panning-von Scheidt, L.: Rig and Engine Validation of the Nonlinear Forced Response Analysis Performed by the Tool OrAgL. J. Eng. Gas Turbines Power 141(2), 9pp, 2018. doi: 10.1115/1.4041160
Groß, J.; Buhl, P.; Weber, U.; Schuler, X.; Krack, M.: Effect of creep on the nonlinear vibration characteristics of blades with interlocked shrouds. International Journal of Non-Linear Mechanics 99, 240-246, 2018. doi: 10.1016/j.ijnonlinmec.2017.12.002
Peter, S.; Scheel, M.; Krack, M.; Leine, R.I.: Synthesis of nonlinear frequency responses with experimentally extracted nonlinear modes. Mechanical Systems and Signal Processing 101, 498-515, 2018. doi: 10.1016/j.ymssp.2017.09.014
Aboulfotoh, N.; Krack, M.; Twiefel, J.; Wallaschek, J.: Experimental Study on Performance Enhancement of a Piezoelectric Vibration Energy Harvester by applying Self-Resonating Behavior. Energy Harvesting and Systems 4(3), 131-136, 2017. doi: 10.1515/ehs-2016-0027
Groß, J.; Schoenenborn, H.; Krack, M.: Analysis of the effect of multi-row and multi-passage aerodynamic interaction on the forced response variation in a compressor configuration – part 2: effects of additional structural mistuning. J. Eng. Gas Turbines Power 140(5), 9pp, 2018. doi: 10.1115/1.4038869
Krack, M.; Aboulfotoh, N.; Twiefel, J.; Wallaschek, J.; Bergman, L.A.; Vakakis, A.F.: Toward understanding the self-adaptive dynamics of a harmonically forced beam with a sliding mass. Archive of Applied Mechanics 87(4), 699–720, 2017. doi: 10.1007/s00419-016-1218-5
Aboulfotoh, N.; Krack, M.; Twiefel, J.; Wallaschek, J.: A Self-Resonant System - Experimental Investigations of Boundary and Operating Conditions. PAMM 16 (1), 253-254, 2016. doi: 10.1002/pamm.201610115
Krack, M.; Salles, L.; Thouverez, F.: Vibration Prediction of Bladed Disks Coupled by Friction Joints. Archives of Computational Methods in Engineering 24(3), 589–636, 2017. doi:10.1007/s11831-016-9183-2
Krack, M.; Panning-von Scheidt, L.; Wallaschek, J.: On the interaction of multiple traveling wave modes in the flutter vibrations of friction-damped tuned bladed disks. J. Eng. Gas Turbines Power 139(4), 9pp, 2016. doi:10.1115/1.4034650
Förster, A.; Krack, M.: An efficient method for approximating resonance curves of weakly-damped nonlinear mechanical systems. Computers and Structures 169, 81-90, 2016. doi:10.1016/j.compstruc.2016.03.003
Krack, M.; Bergman, L.A.; Vakakis, A.F.: On the efficacy of friction damping in the presence of nonlinear modal interactions. Journal of Sound and Vibration 370, 209-220, 2016. doi: 10.1016/j.jsv.2016.01.039
Krack, M.; Bergman, L.A.; Vakakis, A.F.: Absorption of Resonant Vibrations in Tuned Nonlinear Jointed Structures. ASME Journal of Vibration and Acoustics 138(2), 8pp, 2015. doi: 10.1115/1.4032000
Krack, M.; Bergman, L.A.; Vakakis, A.F.: Global complexity effects due to local damping in a nonlinear system in 1:3 internal resonance. Archive of Applied Mechanics 86 (6), 1083-1094, 2015. doi: 10.1007/s00419-015-1080-x
Krack, M.; Bergman, L.A.; Vakakis, A.F.: Motion Complexity in a Non-Classically Damped System with Closely Spaced Modes: From Standing to Traveling Waves. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multibody Dynamics, 13pp, 2015. doi: 10.1177/1464419315593431
Krack, M.: Nonlinear modal analysis of nonconservative systems: Extension of the periodic motion concept. Computers and Structures 154, 59-71, 2015. doi: 10.1016/j.compstruc.2015.03.008
Ertz, G.; Krack, M.; Twiefel, J.: Feasibility Study for Small Scaling Flywheel-Energy-Storage Systems in Energy Harvesting Systems. Energy Harvesting and Systems 1 (3-4), 233–241, 2014. doi: 10.1515/ehs-2013-0010
Krack, M.; Böttcher, J.: A Method for the Computational Assessment of the Damping Performance of Shape Memory Alloys. Smart Materials and Structures 23, 10pp, 2014. doi: 10.1088/0964-1726/23/8/085010
Krack, M.; Tatzko, S.; Panning-von Scheidt, L.; Wallaschek, J.: Reliability Optimization of Friction-Damped Systems Using Nonlinear Modes. Journal of Sound and Vibration 333, 2699–2712, 2014. doi: 10.1016/j.jsv.2014.02.008
Krack, M.; Panning-von Scheidt, L.; Wallaschek, J.: On the Computation of the Slow Dynamics of Nonlinear Modes of Mechanical Systems. Mechanical Systems and Signal Processing 42 (1-2), 71-87, 2013. doi: 10.1016/j.ymssp.2013.08.031
Krack, M.; Panning-von Scheidt, L.; Wallaschek, J.: A Method for Nonlinear Modal Analysis and Synthesis: Application to Harmonically Forced and Self-Excited Mechanical Systems. Journal of Sound and Vibration 332 (25): 6798–6814, 2013. doi: 10.1016/j.jsv.2013.08.009
Krack, M.; Panning-von Scheidt, L.; Wallaschek, J.: A High-Order Harmonic Balance Method for Systems With Distinct States. Journal of Sound and Vibration 332 (21): 5476-5488, 2013. doi: 10.1016/j.jsv.2013.04.048
Krack, M.; Panning-von Scheidt, L.; Wallaschek, J.; Siewert, C.: Hartung, A.: Reduced Order Modeling Based on Complex Nonlinear Modal Analysis and its Application to Bladed Disks With Shroud Contact. J. Eng. Gas Turbines Power 135 (10), 9pp, 2013. doi: 10.1115/1.4025002
Laborenz, J.; Krack, M.; Panning, L.; Wallaschek, J.; Denk, M.: Eddy Current Damper for Turbine Blading: Electromagnetic Finite Element Analysis and Measurement Results. J. Eng. Gas Turbines Power 134(4):8pp, 2012. doi: 10.1115/GT2011-45242
Krack, M.; Secanell, M.; Mertiny, P.: Cost Optimization of a Hybrid Composite Flywheel Rotor With a Split-Type Hub Using Combined Analytical/Numerical Models. Structural and Multidisciplinary Optimization 44(1):57-73, 2011.
Krack, M.; Secanell, M.; Mertiny, P.: Cost Optimization of Hybrid Composite Flywheel Rotors for Energy Storage. Structural and Multidisciplinary Optimization 41(5):779-796, 2010.
Neubauer, M.; Krack, M.; Wallaschek, J.: Parametric Studies on the Harvested Energy of Piezoelectric Switching Techniques. Smart Materials and Structures 19(2):1-10, 2010.
Krack, M.; Gross, J.: Harmonic Balance for Nonlinear Vibration Problems, 159pp, (2019), Springer, ISBN: 978-3-030-14022-9.
Krack, M.; Panning-von Scheidt, L.: Nonlinear Modal Analysis and Modal Reduction of Jointed Structures. The Mechanics of Jointed Structures (2017), Springer, Matthew R.W. Brake (Ed.), ISBN: 978-3-319-56818-8
Krack, M.; Secanell, M.; Mertiny, P.: Rotor Design for High-Speed Flywheel Energy Storage Systems . Energy Storage (2011), IntechOpen, Prof. Rosario Carbone (Ed.), ISBN: 978-953-307-269-2.
Krack, M.; Groß, J.; Scheel, M.; Recent advances on nonlinear vibration analysis using nonlinear modes as reduced basis. IIUTAM Symposium on Model Order Reduction of Coupled Systems, Stuttgart, 2018.
Monjaraz-Tec, C.; Krack, M.; Comparison of Harmonic Balance methods for unilateral contact problems using the massless boundary approach. ECCOMAS, Glasgow, 2018.
Krack, M.; Tutorial: Introduction to Harmonic Balance and application to nonlinear vibrations. ASME Turbo Expo, Oslo, 2018.
Aboulfotoh, N.; Twiefel, J.; Krack, M.; Wallaschek, J.; On the operating conditions of the self-adaptive behavior of a sliding mass along a clamped-clamped beam. GAMM, Munich, 2018.
Scheel, M.; Kleyman, G.; Tatar, A.; Brake, M.; Peter, S.; Noel, J.-P.; Allen, M.; Krack, M.; System Identification of Jointed Structures: Nonlinear Modal Testing vs. State-Space Model Identification. IMAC, Orlando, 2018.
Theurich, T.; Gross, J.; Krack, M.; Suppression of blade vibrations using a nonlinear absorption concept. International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Maui, Hawaii, 2017.
Scheel, M.; Gross, J.; Krack, M.; A Novel Approach for the Experimental NonlinearModal Analysis
of Shrouded Turbine Blades. International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Maui, Hawaii, 2017.
Krack, M. et al.; Effect of creep on the nonlinear vibration characteristics of blades with interlocked shrouds. Blade Mechanics Seminar, Winterthur, Switzerland, 2017.
Scheel, M.; Peter, S.; Leine, R.; Krack, M.; Towards Experimental Nonlinear Modal Analysis of Systems with Nonlinear Damping. European Nonlinear Dynamics Conference (ENOC), Budapest, Hungary, 2017.
Peter, S.; Scheel, M.; Krack, M.; Leine, R.; Experimental Frequency Response Synthesis for Nonlinear Systems. European Nonlinear Dynamics Conference (ENOC), Budapest, Hungary, 2017.
Krack, M.; Bergman, L.A.; Vakakis, A.F.: Self-adaptivity of a beam with sliding mass under harmonic excitation. ECCOMAS, Crete, Greece, 2016.
Aboulfotoh, N.; Krack, M.; Twiefel, J.; Wallaschek, J.: A Self-Resonant System - Experimental Investigations of Boundary and Operating Conditions. PAMM 16 (1), 253-254, 2016. doi: 10.1002/pamm.201610115
Krack, M.; Aboulfotoh, N.; Twiefel, J.; Wallaschek, J.: A Self-Resonant System - Modeling and Theoretical Investigations. GAMM Annual Meeting, Braunschweig, Germany, 2016.
Krack, M.; Bergman, L.A.; Vakakis, A.F.: On the effect of damping on motion complexity and modal interactions in a 2-DOF nonlinear oscillator. ASME IDETC/CIE, Boston, MA, USA, 2015.
Krack, M. et al.; Efficient Vibration Analysis of Friction-Damped Bladed Disks Near Isolated Resonances. Blade Mechanics Seminar, Winterthur, Switzerland, 2014.
Herzog, A.; Krack, M.; Panning-von Scheidt, L.; Wallaschek, J.: Comparison of two widely-used frequency-time domain contact models for the vibration simulation of shrouded turbine blades. Proc. of the ASME Turbo Expo, Düsseldorf, Germany, pp. 1-10, 2014.
Krack, M.; Panning-von Scheidt, L.; Wallaschek, J.: A Framework for the Computational Dynamic Analysis of Coupled Structures Using Nonlinear Modes. Proceedings of the 32nd IMAC, A Conference and Exposition on Structural Dynamics, February 3-5, Orlando, FL, USA, pp. 45-53, 2014.
Krack, M.; Panning-von Scheidt, L.; Wallaschek, J.: A Method of Modal Analysis and Synthesis for Mechanical Systems With Piecewise-Smooth Nonlinearities. Proceedings of 4th Canadian Conference on Nonlinear Solid Mechanics, July 23-26, Montreal, Canada, pp. 1-10, 2013.
Krack, M.; Panning-von Scheidt, L.; Wallaschek, J.; Siewert, C.; Hartung, A.: Analysis and Robust Design of Friction Joints for Vibration Reduction in Bladed Disks. SIRM 2013- 10th International Conference on Vibrations in Rotating Machines, Berlin, Germany, pp. 1-11, 2013.
Krack, M.; Herzog, A.; Panning-von Scheidt, L.; Wallaschek, J.; Siewert, C.; Hartung, A.: Multiharmonic Analysis and Design of Shroud Friction Joints of Bladed Disks Subject to Mircroslip. Proceedings of the ASME IDETC/CIE, Chicago, Il, USA, pp. 1-10, 2012.
Krack, M.; Panning-von Scheidt, L.; Wallaschek, J.; Siewert, C.; Hartung, A.: Robust Design of Friction Interfaces of Bladed Disks with Respect to Parameter Uncertainties. Proceedings of the ASME Turbo Expo, Copenhagen, Denmark, pp. 1-12, 2012.
Krack, M. et al.; Direct Parametric Analysis of the Forced Response of Bladed Disks with Friction Interfaces Using Analytical Contact Models. Blade Mechanics Seminar, Winterthur, Switzerland, 2011.
Krack, M.; Secanell, M.; Mertiny, P.: Advanced Optimization Strategies for Cost-Sensitive Design of Energy Storage Flywheel Rotors. Proceedings of the International SAMPE Symposium and Exhibitions, Seattle, WA, USA, pp. 1-14, 2011.
Siewert, C.; Krack, M.; Panning, L., Wallaschek, J.: The Nonlinear Analysis of the Multiharmonic Forced Response of Coupled Turbine Blading. Proceedings of ISROMAC-12, The 12th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Paper 219, Honolulu, Hawaii, USA, pp. 1-11, 2008.
Contact

Malte Krack
Prof. Dr.-Ing.Head of Structural Mechanics group